Algorithmes de tri, complexité et recherche dichotomique

Les algorithmes de tri sont des algorithmes qui permettent de trier des données. Ils sont très utilisés en informatique, et il en existe de nombreux. Dans ce cours, nous allons voir les plus connus pour comprendre leur fonctionnement et leur intérêt.

Comment trier un tableau de nombres ? C'est une question qui peut paraître simple, mais qui est en fait assez complexe. Il existe de nombreux algorithmes de tri, et chacun a ses avantages et ses inconvénients.

Tri par comparaison

Les premiers algorithmes de tri que nous allons voir sont des algorithmes de tri par comparaison (Comparison based strategies).

Ils consistent à comparer deux à deux les éléments du tableau puis de les échanger ou non en fonction du résultat de la comparaison.

Tri par sélection (selection sort)

L'algorithme de tri par sélection est un algorithme de tri qui consiste à trouver le plus petit élément du tableau, et à le placer en première position (ou le plus grand élément en dernière position). On répète cette opération jusqu'à ce que le tableau soit trié.

Un exemple, avec le tableau suivant [6, 2, 8, 1, 5, 3, 9]:

1. On, parcourt le tableau pour trouver le plus petit élément qui est 1.

   Son indice est 3, on l'échange avec l'élément à l'indice 0 (le premier élément du tableau).

   1

   2

   8

   6

   5

   3

   9

   Le premier élément du tableau est désormais le plus petit élément du tableau. On recommence l'opération, mais en ignorant le premier élément du tableau, car il est déjà trié.

   info

   Toute l'astuce de cet algorithme est donc de trier un sous-tableau plus petit à chaque itération jusqu'à ce que le tableau soit trié.

Voilà les itérations suivantes:

1. Le deuxième plus petit élément est 2, il est déjà à la bonne place, on ne fait rien.

2. 1

   2

   3

   6

   5

   8

   9

3. 1

   2

   3

   5

   6

   8

   9

4. Il reste trois éléments à trier ([6, 8, 9]), il sont déjà triés, on ne fait rien.

Voilà, le tableau est trié.

Je t'invite à regarder le fonctionnement de cet algorithme sur cette animation ou encore ici (clique sur "SEL" ou "Selection Sort" dans la barre de navigation).

Tri à bulles (bubble sort)

Le tri à bulles est un autre algorithme de tri très connu. Il consiste à comparer deux à deux les éléments du tableau, et à les échanger si ils ne sont pas dans le bon ordre. On répète cette opération jusqu'à ce que le tableau soit trié.

remarque

Cela va avoir pour effet de faire "remonter" les plus grands éléments du tableau vers la fin du tableau, comme des bulles d'air qui remontent à la surface.

Un exemple, avec le même tableau [6, 2, 8, 1, 5, 3, 9]:

1. On compare les deux premiers éléments du tableau, 6 et 2. Comme 6 est plus grand que 2, on les échange.

   2

   6

   8

   1

   5

   3

   9

On recommence l'opération avec les deux éléments suivants, 6 et 8. Comme 6 est plus petit que 8, on ne fait rien. On procède ainsi jusqu'à la fin du tableau.

On obtient après un premier passage sur l'ensemble du tableau:

2

6

1

5

3

8

9

On recommence l'opération, mais en ignorant le dernier élément du tableau, car il est déjà trié.

Voilà les itérations suivantes:

1. 2

   1

   5

   3

   6

   8

   9

2. 1

   2

   3

   5

   6

   8

   9

3. Dernier passage, aucun échange n'est effectué. Le tableau est trié.

Parlons un peu de complexité

La complexité d'un algorithme est une mesure de la quantité de ressources (temps, mémoire, etc) que celui-ci va utiliser pour s'exécuter.

En général, on s'intéresse à la complexité en fonction de la taille des données en entrée de l'algorithme.

Il existe plusieurs types de complexité, la plus souvent utilisée est la complexité en temps.

Cela revient à se poser la question:

Si je donne à mon programme une entrée de taille n, quel est l'ordre de grandeur (en fonction de n) du nombre d'opérations qu'il va effectuer ?

remarque

La complexité permet de quantifier la relation entre les conditions de départ et le temps effectué par l'algorithme.

Opérations de base

Pour "compter les opérations", il faut décider de ce qu'est une opération. Ce choix dépend du problème (et même de l'algorithme) considéré. Il faut en fait choisir soi-même quelques petites opérations que l'algorithme effectue souvent, et que l'on veut utiliser comme opérations de base pour mesurer la complexité. Les opérations qui caractérisent le mieux l'algorithme et représentent le mieux le temps d'exécution de celui-ci. Les opérations de base sont souvent les opérations arithmétiques, les comparaisons, les affectations, etc. Par exemple, pour un algorithme de tri, on va compter le nombre de comparaisons et d'échanges d'éléments du tableau.

En fonction des algorithmes, certaines opérations peuvent être plus significatives que d'autres. Par exemple, la multiplication est plus coûteuse que l'addition, on peut donc ne considérer que les opérations de multiplication pour mesurer la complexité d'un algorithme.

info

On ne compte pas les opérations qui ne dépendent pas de la taille des données en entrée (comme l'initialisation de variables, etc). Ces opérations sont considérées comme constantes et pas significatives pour la complexité en fonction de la taille des données en entrée.

Notation "grand O"

On exprime la complexité en fonction de la taille des données en entrée avec la notation "grand O". La notation "grand O" est une notion mathématique qui permet d'exprimer un ordre de grandeur.

Par exemple, des algorithmes effectuant environ $n$ opérations, $2n+20$ opérations ou $n/2$ opérations ont tous la même complexité : on la note $O(n)$ (lire "grand O de $n$"). De même, un algorithme en $3n^2 + 4n + 2$ opérations aura une complexité de $O(n^2)$ : on néglige les termes de plus faible degré (ici $4n$ et $2$) et les coefficients (ici $3$). On cherche seulement à savoir comment évolue le nombre d'opérations en fonction de la taille des données en entrée et on considère le terme de plus haut degré qui est celui qui va croître le plus vite en fonction de la taille des données en entrée.

VOilà un graphique récapitulatif des différentes notations "grand O" communes:

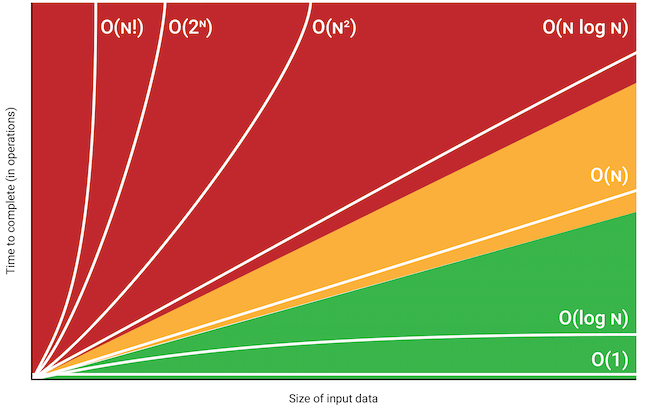
Exemple de calcul de complexité

Prenons l'exemple du tri par sélection.

Pour trier un tableau de taille $n$, premièrement on parcourt le tableau pour trouver le plus petit élément, on va donc effectuer $n$ comparaisons.

Ensuite, on va échanger cet élément avec le premier élément du tableau, on va donc effectuer $1$ échange.

Ensuite on va recommencer l'opération, mais en ignorant le premier élément du tableau, car il est déjà trié.

On va donc effectuer $n-1$ comparaisons et $1$ échange.

On va faire cela jusqu'à ce que le tableau soit trié, donc jusqu'à ce qu'il ne reste plus qu'un seul élément à trier.

Pour résumer, on va effectuer pour les différentes itérations:

• $n$ comparaisons et $1$ échange
• $n-1$ comparaisons et $1$ échange
• $n-2$ comparaisons et $1$ échange
• ...
• $1$ comparaison et $1$ échange

On peut donc calculer le nombre total de comparaisons et d'échanges effectués par l'algorithme:

$$\begin{align*} = & (n+1) + ((n-1)+1) + ((n-2)+1) + ... + (1+1) \\ = & (n + (n-1) + \dots + 1) + (1 + \dots + 1) \\ = & \frac{n(n+1)}{2} + n \\ = & \frac{n^2 + 3n}{2} \\ \end{align*}$$

Ici, j'ai compté de manière exacte le nombre d'opérations effectuées par l'algorithme, mais en général on s'intéresse à la complexité en fonction de la taille des données en entrée.

On va donc garder uniquement le terme de plus haut degré, ici $n^2$.

On dit que la complexité du tri par sélection est en $O(n^2)$.

info

On peut aussi évaluer cette complexité sans calcul exact, mais plutôt en estimant le nombre d'opérations effectuées par l'algorithme.

On peut voir que l'algorithme doit à chaque itération parcourir le tableau, c'est ce qui va prendre le plus de temps et dépendra de la taille du tableau.

Chaque itération va permettre de trier un élément du tableau, donc on va effectuer $n$ itérations.

On peut donc estimer que la complexité du tri par sélection est en $O(n \times n) = O(n^2)$.

Complexité dans le pire des cas

Le nombre d'opérations effectuées par un algorithme peut dépendre de la taille des données en entrée, mais aussi des données elles-mêmes.

Par exemple, dans le cadre d'un tri à bulles, si le tableau est déjà trié, on n'effectuera aucune opération d'échange, et seulement $n$ comparaisons.

On peut donc dire que la complexité du tri à bulles est en $O(n)$ dans le meilleur des cas.

Mais si le tableau est trié dans l'ordre inverse, on va effectuer $n$ comparaisons et $n$ échanges à chaque itération, et on va effectuer $n$ itérations.

On peut donc dire que la complexité du tri à bulles est en $O(n \times n) = O(n^2)$ dans le pire des cas.

remarque

C'est intéressant de considérer la complexité dans le pire des cas, car elle permet de savoir si l'algorithme est efficace pour toutes les données possibles. En général pour des données quelconques, c'est en général assez proche du comportement dans le pire des cas.

Complexité en moyenne

On peut aussi s'intéresser à la complexité en moyenne, c'est-à-dire la complexité sur toutes les données possibles.

Par exemple, pour le tri à bulles, la complexité en moyenne est en $O(n^2)$.

Il existe des algorithmes qui ont une complexité en moyenne bien meilleure que leur complexité dans le pire des cas. Cela dépend du problème considéré et demande une analyse plus fine de l'algorithme.

Complexité en mémoire

On peut aussi s'intéresser à la complexité en mémoire d'un algorithme. Autrement dit, combien de mémoire va utiliser l'algorithme en fonction de la taille des données en entrée.

C'est aussi une mesure de la complexité pertinente.

Si par exemple on a besoin de trier un tableau de 1000 éléments, on peut se dire que la complexité en temps n'est pas très importante, car l'algorithme va s'exécuter très rapidement. Mais si l'algorithme utilise beaucoup de mémoire, cela peut poser problème, car il peut ne pas avoir assez de mémoire disponible pour exécuter l'algorithme.

Dans la plupart des cas, la complexité en mémoire est beaucoup plus simple à calculer que la complexité en temps.

Mais dans des problèmes plus compliqués, la complexité en mémoire et la complexité en temps peuvent être liées.

On peut par exemple choisir de sacrifier un peu de rapidité d'exécution pour utiliser moins de mémoire, ou au contraire d'augmenter la vitesse en augmentant la complexité en mémoire de notre algorithme, par exemple en stockant dans un tableau les résultats déjà calculés (c'est le principe de la mise en cache, appelée aussi memoization).

remarque

De nos jours, la complexité en mémoire est moins importante qu'avant, car les ordinateurs ont beaucoup de mémoire disponible. Dans la majorité des cas, on va donc plutôt s'intéresser à la complexité en temps. Mais la complexité en mémoire reste importante dans certains cas avancés ou avec des données très volumineuses.

Limitation de la complexité

La complexité d'un algorithme est donc une mesure d'ordre de grandeur en fonction de la taille des données en entrée.

Cependant, il est important de garder à l'esprit que la complexité ne permet pas de savoir si un algorithme est rapide ou lent.

Même si un algorithme à une complexité plus faible qu'un autre, il peut être plus (beaucoup plus) lent à s'exécuter qu'un autre algorithme pour des tailles de données en entrée faibles.

Tri diviser pour régner (Divide-and-Conquer paradigm)

Il existe d'autres algorithmes de tri plus efficaces que les algorithmes de tri par comparaison. Ils sont basés sur le principe de diviser pour régner (divide and conquer en anglais). L'idée est de diviser le problème en sous-problèmes plus petits, de résoudre les sous-problèmes, puis de fusionner les solutions des sous-problèmes pour résoudre le problème initial.

Tri fusion (merge sort)

Le tri fusion est un algorithme de tri qui consiste à diviser le tableau en deux parties égales, trier les deux parties, puis fusionner les deux parties triées.

Il y a donc deux "phases" dans cet algorithme:

• la phase de division du tableau en deux parties égales
• la phase de fusion des deux parties triées

Phase de division

Pour la phase de division, on va choisir de diviser et trier le tableau en deux parties égales pour maximiser l'efficacité de l'algorithme (ou presque égales si le tableau a une taille impaire).

Il existe deux façons de procéder pour cibler les deux parties du tableau:

• Créer des tableaux intermédiaires pour stocker les deux parties du tableau à trier.
• Utiliser des indices pour définir les parties du tableau à trier, et trier directement le tableau en place.

La première méthode est plus simple à comprendre, mais utilise plus de mémoire, car il faut créer des tableaux intermédiaires (allocation de mémoire supplémentaire).

En pratique, on privilégie donc la deuxième méthode, et c'est celle que je vais détailler ici.

Pour trier un tableau, on va donc utiliser deux indices, un indice de début et un indice de fin, qui vont définir la partie du tableau à trier.

Par exemple, pour le tableau [6, 2, 8, 1, 5, 3, 9], les indices 0 et 6 vont définir le tableau complet. On va calculer la taille de la partie du tableau à trier, ici 6 (indice de fin) - 0 (indice de début) + 1 (car on compte l'élément à l'indice de fin), soit 7.

On va ensuite diviser cette taille par deux, soit 3 (on peut arrondir à l'entier inférieur).

On va donc trier les deux parties [6, 2, 8, 1] (des indices 0 à 3) et [5, 3, 9] (des indices 4 à 6). Enfin, la fusion des deux parties triées va permettre d'obtenir le tableau trié.

info

Cela fonctionne à condition que l'algo de tri que l'on va utiliser pour trier les deux sous-tableaux fonctionne "in-place", c'est-à-dire qu'il trie directement le tableau en place sans utiliser de tableau intermédiaire.

Phase de fusion

C'est la phase de fusion qui est la plus intéressante, car c'est elle qui va permettre réellement de trier le tableau.

Dans cette phase de fusion il est plus simple de copier les éléments dans deux sous-tableaux intermédiaires, puis d'écrire les éléments triés dans le tableau final directement.

info

Il existe des méthodes pour effectuer cette fusion sans copier les éléments dans des tableaux intermédiaires, mais elles sont bien plus complexes à mettre en oeuvre.

Pour fusionner deux tableaux triés, on va utiliser deux (autres) indices, un indice pour chaque sous-tableau, qui vont permettre de parcourir les deux tableaux et de pointer vers les éléments les plus petits des deux tableaux.

On va comparer les deux éléments les plus petits des deux tableaux, et ajouter le plus petit des deux dans le tableau final.

On va incrémenter l'indice du tableau dont on a ajouté l'élément, et on recommence l'opération jusqu'à ce qu'on ait parcouru les deux tableaux.

attention

Il faut faire attention à ne pas dépasser la taille des sous-tableaux avec les indices, sinon on va avoir une erreur en essayant d'accéder à un élément qui n'existe pas.

Il faut donc vérifier que les indices sont bien inférieurs à la taille des sous-tableaux.

Si l'un des deux indices est égal à la taille du sous-tableau, cela veut dire qu'on a parcouru tout le sous-tableau, et qu'il ne reste plus qu'à ajouter les éléments du deuxième sous-tableau dans le tableau final.

On obtient ainsi un tableau trié.

info

La condition d'arrêt de la récursion est quand la taille de la partie du tableau à trier est inférieure ou égale à 1, car un tableau de taille 1 est déjà trié (de même pour un tableau vide).

Récursion

Dans l'exemple précédent, je n'ai pas détaillé la phase de tri des deux sous-tableaux, on pourrait par exemple utiliser un tri précédemment vu comme le tri par sélection pour trier les deux sous-tableaux.

Cela améliorerait la complexité de l'algorithme mais pas la tendance asymptotique de l'algorithme. En reprenant les calculs précédents (où on avait $\frac{n^2 + 3n}{2}$ comparaisons et d'échanges), cela nous donnerait:

$$\begin{align*} = & \frac{(\frac{n}{2})^2 + 3(\frac{n}{2})}{2} * 2 \\ = & \frac{n^2}{4} + 3(\frac{n}{2}) \\ \end{align*}$$

C'est bien inférieur à la complexité du tri par sélection initial, mais cela reste en $O(n^2)$.

Mais on pourrait très bien de nouveau utiliser le tri fusion pour trier les sous-tableaux, et ainsi de suite.

L'algorithme de tri fusion est un algorithme récursif, c'est-à-dire qu'il s'appelle lui-même pour trier les sous-tableaux.

Cela reviens à diviser le tableau en deux parties égales, puis chaque partie en deux parties égales, etc, jusqu'à ce qu'on ait des sous-tableaux de taille 1 ou 0 puis fusionner les sous-tableaux 2 à 2 pour obtenir le tableau trié.

C'est un algorithme très efficace, en faisant cela, on va trier le tableau en $O(n \log n)$ opérations, ce qui est beaucoup plus efficace que les algorithmes de tri par comparaison.

info

Il est plus efficace cependant les copies effectuées pour l'étape de fusion des tableaux intermédiaires triés peuvent être coûteuses et impacter la complexité (en mémoire) de l'algorithme.

On va découvrir un autre algorithme de tri qui à la même complexité en temps que le tri fusion mais qui ne nécessite pas de copies intermédiaires (En TDs, si vous les implémentez tout les deux je vous suggère de comparer les deux algorithmes pour vous rendre compte de la différence de performance).

Tri rapide (quick sort)

Le tri rapide est un algorithme de tri qui consiste à choisir un élément du tableau, appelé pivot, et à placer tous les éléments plus petits que le pivot à gauche du pivot, et tous les éléments plus grands que le pivot à droite du pivot.

On répète ensuite l'opération sur les deux sous-tableaux, jusqu'à ce que le tableau soit trié.

De la même manière que pour le tri fusion, c'est un algorithme récursif et on va donc utiliser des indices pour définir les parties du tableau à trier.

Il y a également deux phases dans cet algorithme:

• la phase de division du tableau en deux parties en fonction du pivot
• la phase de tri des deux parties

Phase de division

Choix du pivot

Le choix du pivot est très important, car il va déterminer la complexité de l'algorithme.

Si on choisit un pivot qui est toujours le plus petit élément du tableau, on va avoir une complexité en $O(n^2)$, car on va devoir parcourir tout le tableau à chaque itération (de même si on choisit le plus grand élément du tableau).

Il existe plusieurs méthodes pour choisir le pivot, la plus simple est de choisir le premier ou le dernier élément du tableau. Mais cela peut être problématique si le tableau est déjà trié car on va diviser le tableau en deux parties de tailles très différentes.

info

L'idéal est de choisir un pivot qui est proche de la valeur médiane du tableau, c'est-à-dire qui va diviser le tableau en deux parties égales.

Il existe plusieurs méthodes pour choisir un pivot proche de la valeur médiane du tableau, mais elles sont plus compliquées à mettre en oeuvre.

Partitionnement

Une fois le pivot choisi, on va parcourir le tableau et placer tous les éléments plus petits que le pivot à gauche du pivot, et tous les éléments plus grands que le pivot à droite du pivot.

Il y a plusieurs approches pour gérer le pivot, dans notre cas, on va choisir de premièrement placer le pivot à la fin du tableau. Ou tout simplement choisir le pivot comme étant le dernier élément du tableau.

On va s'aider d'un indice qui va nous indiquer le premier élément plus grand que le pivot et qui va nous permettre de placer le pivot à sa place définitive.

On va ensuite parcourir le tableau pour placer les éléments plus petits que le pivot à gauche du pivot, et les éléments plus grands que le pivot à droite du pivot.

Si l'élément que l'on parcourt est plus petit que le pivot, on va l'échanger avec l'élément à l'indice du premier élément plus grand que le pivot, et on va incrémenter l'indice du premier élément plus grand que le pivot.

Une fois qu'on a parcouru tout le tableau, on va échanger le pivot avec l'élément à l'indice du premier élément plus grand que le pivot pour que le pivot soit à sa place définitive (entre les éléments plus petits et les éléments plus grands).

Enfin, on va renvoyer l'indice du pivot pour pouvoir appeler récursivement l'algorithme sur les deux sous-tableaux.

Récursion

On obtient ainsi un tableau avec le pivot à sa place définitive, et tous les éléments plus petits que le pivot à gauche du pivot, et tous les éléments plus grands que le pivot à droite du pivot et on connaît l'indice du pivot.

On va donc pouvoir appeler récursivement l'algorithme sur les deux sous-tableaux, en ignorant la place du pivot.

Tri par dénombrement (counting sort)

IL existe encore d'autres algorithmes de tri, mais ils sont plus spécifiques et ne fonctionnent que dans certains cas. Je vais en présenter un simple ici pour vous donner une idée de ce qui existe.

Le tri par dénombrement (ou counting sort en anglais) est très efficace, car il va permettre de trier un tableau en complexité linéaire, c'est-à-dire en $O(n)$. Il ne fonctionne cependant que pour des données entières car il ne se base pas sur des comparaisons mais va compter le nombre d'occurrences de chaque valeur (de plus pour simplifier, on va supposer que les valeurs sont positives).

Le prérequis pour utiliser cet algorithme est donc de connaître la valeur maximale des données à trier. Soit on connaît cette valeur à l'avance, soit on peut la calculer en parcourant le tableau une première fois.

L'algorithme consiste à compter le nombre d'occurrences de chaque valeur dans le tableau, puis à reconstruire le tableau en plaçant les valeurs dans l'ordre.

Par exemple, si on se fixe des valeurs entières entre 0 et 9, on peut trier le tableau suivant [1, 4, 1, 2, 7, 5, 2] en procédant ainsi:

1. On parcourt le tableau pour compter le nombre d'occurrences de chaque valeur.

valeur	0	1	2	3	4	5	6	7	8	9
nombre d'occurrences	0	2	2	0	1	1	0	1	0	0

2. On reconstruit le tableau en parcourant le tableau des occurrences et en ajoutant les valeurs dans l'ordre.

• On ajoute 2 fois la valeur 1
• On ajoute 2 fois la valeur 2
• ...

On obtient ainsi le tableau trié [1, 1, 2, 2, 4, 5, 7].

attention

On remarque qu'il faut pouvoir stocker le nombre d'occurrences de chaque valeur, donc un tableau de taille 10 dans notre exemple. Il faut donc un tableau de taille $k$ pour trier des données comprises entre 0 et $k-1$ ce qui augmente la complexité en mémoire de l'algorithme.

C'est à prendre en compte si on veut utiliser cet algorithme car il peut être très efficace en temps, mais peut aussi utiliser beaucoup de mémoire si les valeurs sont très grandes.

C'est un algorithme à utiliser seulement dans le cas où on connaît la valeur maximale des données à trier et que cette valeur est raisonnable.

Pour aller plus loin:

Tri par dénombrement stable

Details

On peut améliorer le tri par dénombrement en le rendant stable. Cela signifie que si deux éléments ont la même valeur, ils seront dans le même ordre dans le tableau trié que dans le tableau initial. Cela ne semble pas très important à première vue, mais cela permet de trier des données plus complexes en leur associant des valeurs entières sur lesquelles on va effectuer le tri.

Pour faire cela il faut modifier légèrement l'algorithme de tri par dénombrement.

Une fois qu'on a compté le nombre d'occurrences de chaque valeur, on va calculer la somme partielle des occurrences de chaque valeur. Cela va nous permettre de connaître la position de chaque valeur dans le tableau trié.

Par exemple, avec le tableau suivant [1, 4, 1, 2, 7, 5, 2] contenant des valeurs entières entre 0 et 9:

• On compte le nombre d'occurrences de chaque valeur : [0, 2, 2, 0, 1, 1, 0, 1, 0, 0]
• On calcule la somme partielle des occurrences de chaque valeur : [0, 2, 4, 4, 5, 6, 6, 7, 7, 7]

remarque

On peut se resservir du tableau des occurrences pour stocker la somme partielle des occurrences de chaque valeur, ce qui permet de ne pas utiliser de tableau intermédiaire supplémentaire.

On va construire un nouveau tableau de même taille que le tableau initial, en parcourant le tableau initial pour ajouter les valeurs dans le nouveau tableau. On va ajouter la valeur à la position indiquée par la somme partielle des occurrences de la valeur, puis on va décrémenter la somme partielle des occurrences de la valeur.

Par exemple, pour la valeur 1, on va ajouter la valeur 1 à la position 2 du nouveau tableau, puis on va décrémenter la somme partielle des occurrences de la valeur 1 pour obtenir 1 (car il reste une occurrence de la valeur 1).

On obtient ainsi le tableau trié [1, 1, 2, 2, 4, 5, 7].

L'inconvénient principal de cette méthode est qu'il faut un tableau intermédiaire pour stocker le tableau trié, ce qui augmente la complexité en mémoire de l'algorithme.

Tri par base (radix sort)

Details

Le tri par dénombrement permet de trier des données entières comprises entre 0 et $k-1$ en complexité linéaire.

On va se servir de cet algorithme pour trier des données plus complexes, en associant à chaque donnée une valeur entière sur laquelle on va effectuer le tri (d'où l'intérêt de rendre le tri par dénombrement stable).

On va considérer un tri de nombres entiers, mais cela peut s'appliquer à d'autres types de données.

Un nombre entier peut être représenté en base 10, c'est-à-dire en utilisant les chiffres de 0 à 9.

Par exemple, le nombre 123 peut être représenté en base 10 par la suite de chiffres 1, 2 et 3.

On va donc pouvoir trier des nombres entiers en triant les chiffres de leur représentation en base 10.

Par exemple, pour trier les nombres [123, 456, 324, 682, 789, 118, 321, 654, 987], on va trier les chiffres des nombres, en commençant par les unités, puis les dizaines, puis les centaines.

Cela permet de trier les nombres en complexité linéaire grâce au tri par dénombrement.

Dans notre exemple, le nombre le plus grand est 987, il a donc 3 chiffres, on va donc effectuer 3 itérations de tri par dénombrement pour trier les nombres.

remarque

Cette information peut être connue à l'avance, mais on peut aussi la calculer en parcourant le tableau une première fois.

1. On trie les unités ce qui donne [321, 682, 123, 324, 654, 456, 987, 118, 789]
2. On trie les dizaines ce qui donne [118, 321, 123, 324, 456, 654, 682, 987, 789]
3. enfin, on trie les centaines ce qui donne [118, 123, 321, 324, 456, 654, 682, 789, 987]

Recherche dichotomique

Avoir un tableau trié est très utile pour effectuer des recherches dans un tableau.

Par exemple, si on veut savoir si une valeur est présente dans un tableau, on peut le parcourir le tableau et comparer chaque élément avec la valeur recherchée.

Mais si le tableau est trié, on peut utiliser une méthode plus efficace: la recherche dichotomique.

La recherche dichotomique consiste à diviser le tableau en deux parties égales et à ne garder que la partie qui contient la valeur recherchée. On répète l'opération jusqu'à trouver la valeur ou jusqu'à ce qu'il ne reste plus qu'un seul élément dans le tableau.

Exemple simple avec le tableau suivant [1, 2, 2, 4, 5, 8, 12] (nombre d'éléments: 7) et la valeur recherchée 8:

1. On calcule l'indice du milieu du tableau, soit 3.

   On compare la valeur à l'indice 3 avec la valeur recherchée 8, comme 4 est plus petit que 8, on ne garde que la partie du tableau qui contient la valeur recherchée, c'est-à-dire la partie du tableau à partir de l'indice 4 (indice de début: 4, indice de fin: 6).

   On recommence l'opération avec la partie du tableau restante.

2. Sous partie du tableau: [5, 8, 12] (nombre d'éléments: 3), indice du milieu: 5.

   On compare la valeur à l'indice 5 avec la valeur recherchée 8, comme 8 est égal à 8, on a trouvé la valeur recherchée.

   On peut donc s'arrêter et renvoyer l'indice 5.

Complexité

La complexité de la recherche dichotomique est en $O(log(n))$.

(où $log$ est le logarithme en base 2 et pas $ln$ qui est le logarithme népérien)

En effet, à chaque itération, on divise le tableau en deux parties égales, ce qui permet de réduire la taille du tableau à chaque itération.

On peut donc calculer le nombre d'itérations nécessaires pour trouver la valeur recherchée en fonction de la taille du tableau.

Par exemple, pour un tableau de taille 8, on va effectuer au maximum 3 itérations pour trouver la valeur recherchée.

• On divise le tableau en deux parties égales, on ne garde que la partie qui contient la valeur recherchée, soit 4 éléments.
• On divise le tableau en deux parties égales, on ne garde que la partie qui contient la valeur recherchée, soit 2 éléments.
• In reste 2 elements (dernière itération). On garde la valeur recherchée.

Ce qui fait un total de $log_2(8) = 3$ itérations.

Résumé

• Les algorithmes de tri sont très importants en informatique, car ils permettent de trier des données, ce qui est une opération très courante.
• La complexité d'un algorithme est une mesure de la quantité de ressources (temps, mémoire, etc) que celui-ci va utiliser pour s'exécuter.
• La complexité en temps permet de quantifier la relation entre les conditions de départ (nombre d'éléments du tableau, valeurs des éléments, etc) et le temps effectué par l'algorithme.
• La complexité permet de savoir quel algorithme est le plus efficace quand on a un très grand nombre de données, mais ne permet pas de savoir si un algorithme est rapide ou lent pour un petit nombre de données (un algorithme avec une complexité en $O(n^2)$ peut être plus rapide qu'un algorithme avec une complexité en $O(n \times log(n))$ pour un petit nombre de données).
• Nous avons vu les algorithmes de tri suivants:
  • Tri par sélection (selection sort): $O(n^2)$

    C'est un algorithme qui fonctionne par recherche successive du plus petit élément du tableau.

  • Tri à bulles (bubble sort): $O(n^2)$

    C'est un algorithme qui fonctionne par comparaison successive de deux éléments consécutifs du tableau.

  • Tri fusion (merge sort): $O(n \times log(n))$

    C'est un algorithme qui fonctionne par récursion en divisant le tableau en deux parties égales, en triant les deux parties, puis en fusionnant les deux parties triées.

  • Tri rapide (quick sort): $O(n \times log(n))$

    C'est un algorithme qui fonctionne par récursion en choisissant un pivot, en divisant le tableau en deux parties en fonction du pivot, puis en triant les deux parties.

  • Tri par dénombrement (counting sort): $O(n)$

    C'est un algorithme qui fonctionne en comptant le nombre d'occurrences de chaque valeur, puis en reconstruisant le tableau en plaçant les valeurs dans l'ordre. C'est un algorithme qui ne fonctionne que pour des données entières et où la valeur maximale des données est connue à l'avance et relativement petite.

• La recherche dichotomique est une méthode de recherche dans un tableau trié qui consiste à diviser le tableau en deux parties égales et à ne garder que la partie qui contient la valeur recherchée. On répète l'opération jusqu'à trouver la valeur souhaitée.